Advent of Code 2025 - Day 2: Gift Shop

Day 2 brought a pattern-matching problem in the gift shop database. The task was to identify “invalid” product IDs - numbers that consist of a repeating sequence of digits.

Part 1: Finding Doubled Patterns

The first part required finding numbers where a sequence repeats exactly twice: 11 (5 repeated twice), 1010 (10 repeated twice), 123123 (123 repeated twice), etc.

My approach was regex-first. I default to regex when pattern matching is involved because it’s expressive and, when it works, elegant. I always think back at:

The strategy:

1. Parse comma-separated ranges (turns out my helper library didn’t have a proper CSV loader, so I wrote loadList())
2. Split each range like “11-22” into start and end integers
3. Iterate through every number in the range
4. Filter for even-length numbers (odd-length numbers can’t be evenly split)
5. Use regex ^(.+)\1$ to match doubled patterns

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def part1():
    arr = loadList(input_f)
    score = 0
    for a in arr:
        nums = list2int(re.split(r'-',a))
        for x in range(nums[0],nums[1]+1):
            val = re.fullmatch(r'^(.+)\1$',str(x))
            if len(str(x)) % 2 == 0:
                if val != None:
                    score += int(val.group(0))
    return score

The regex ^(.+)\1$ works by:

• (.+) captures one or more digits
• \1 matches exactly what was captured
• ^ and $ ensure the entire string matches

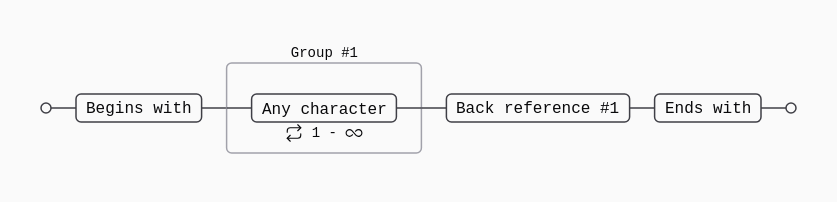
First try. But slower than I expected around 2400ms.

Part 2: Repeating Two or More Times

Part 2 expanded the definition: now any sequence repeated two or more times counts as invalid. So 123123123 (three times) or 1111111 (seven times) are invalid too.

The modification was minimal:

• Remove the even-length check (since patterns can repeat any number of times)
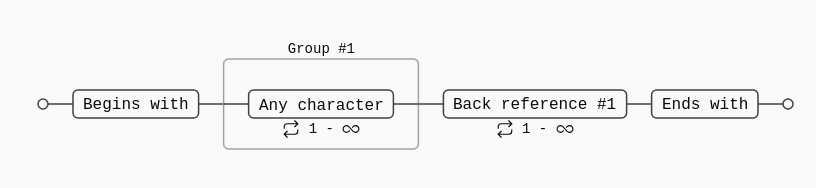
• Change regex from ^(.+)\1$ to ^(.+)\1+$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def part2():
    arr = loadList(input_f)
    score = 0
    for a in arr:
        nums = list2int(re.split(r'-',a))
        for x in range(nums[0],nums[1]+1):
            val = re.fullmatch(r'^(.+)\1+$',str(x))
            if val != None:
                score += int(val.group(0))
    return score

The + after \1 means “one or more additional matches,” so the pattern matches 2+ repetitions instead of exactly 2.

Got it first try too. Performance was still about 2400ms.

Performance Thoughts

The solution works but isn’t fast. Converting every number to a string and running regex on it adds up when you’re checking thousands of numbers per range. There’s probably a mathematical approach that would be faster - maybe something involving string length divisors and modulo arithmetic to check if a number equals itself repeated.

But for Advent of Code puzzle sizes, 2 seconds is fine. The code is readable, the regex is clean, and both parts were first-attempt solves. Sometimes that matters more than shaving milliseconds.

Attempting to Optimize

After solving both parts (and thinking of the puzzle throughout the day), I thought about whether there was a faster approach than regex. The logic seemed straightforward:

1. For each number, try possible block sizes (1 up to half the number’s length)
2. Extract the first block of that size
3. Repeat it and check if it equals the original number
4. If it matches, we found a repeating pattern

The implementation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def part2():
    arr = loadList(input_f)
    score = 0
    for a in arr:
        nums = list2int(re.split(r'-',a))
        for x in range(nums[0],nums[1]+1):
            str_len = len(str(x))
            block = str_len // 2
            for y in range(1,block+1):
                if str_len % y != 0:  # Skip if block doesn't divide evenly
                    continue
                repeats = str_len // y
                if repeats < 2:
                    continue
                
                r = str(x)[:y]*repeats 
                if r == str(x):
                    score += x
                    break
    return score

The theory was sound - only test block sizes that divide evenly into the total length, skip patterns that wouldn’t repeat at least twice. Should be faster, right?

Results:

• Original regex version: ~2400ms
• “Optimized” version: ~4000ms
• With the modulo check: ~3000ms

The optimization made it slower.

The reason? Probably because Python’s regex engine is implemented in highly optimized C code. My pure-Python string slicing, multiplication, and comparison logic couldn’t compete with that, even with the theoretical algorithmic improvements.

This is a good reminder that “fewer operations” doesn’t always mean “faster code” when you’re comparing interpreted Python loops to compiled C regex operations. Sometimes the simple, readable solution is also the fast one.

The Actual Optimization

After the failed attempt to beat regex with pure Python, I realized there was a simpler optimization: compile the regex pattern once instead of recompiling it on every iteration.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def part2_simpler():
    arr = loadList(input_f)
    score = 0
    for a in arr:
        nums = list2int(re.split(r'-', a))
        pattern = re.compile(r'^(.+)\1+$')  # Compile once per range
        for x in range(nums[0], nums[1] + 1):
            if pattern.fullmatch(str(x)):
                score += x
    return score

Results:

• Original: ~2400ms
• With compiled regex: ~1200ms

Nearly 2x faster. The issue with the original code was that re.fullmatch(r'^(.+)\1+$', str(x)) was parsing and compiling the regex pattern on every single number check. By compiling it once with re.compile() and reusing the compiled pattern object, we eliminate that overhead.

This is the right kind of optimization - still using the fast C-based regex engine, just removing unnecessary repeated work. It’s a good reminder that sometimes the best optimization isn’t a clever algorithm rewrite, but just understanding what your existing code is doing under the hood.

Two more stars collected.